The following technical discussion is part of an occasional series showcasing the ISA Mentor Program, authored by Greg McMillan, industry consultant, author of numerous process control books, 2010 ISA Life Achievement Award recipient and retired Senior Fellow from Solutia Inc. (now Eastman Chemical). Greg will be posting questions and responses from the ISA Mentor Program, with contributions from program participants.
In the ISA Mentor Program, I am providing guidance for extremely talented individuals from countries such as Argentina, Brazil, Malaysia, Mexico, Saudi Arabia, and the USA. This question is from Héctor Torres, an original member of the ISA Mentor Program, with my answer and additional input from program participants Hunter Vegas (project engineering manager at Wunderlich-Malec) and Michel Ruel (executive director, engineering practice at BBA Inc.)
Hector Torres is a senior process and control engineer for Eastman Chemical Company in Tlaxcala, Mexico, with more than 20 years of experience.
The PID controller has been used in more than 99 percent of the control loops in the process industry for the last 80-plus years. The loop performs only as well as the controller is tuned. Considerable confusion exists as to how the PID Form affects tuning settings. The lack of understanding of Form and units of settings can lead to disastrous results. Users may not realize that the algorithm shown in text books often implies an Independent Form that is also known as the Parallel Form and consequential engineering units that are seldom used in the process industry. Some of these algorithms even imply the PID computation is done in engineering units rather than in percent of input and output scales that is almost universally done in industry. The lack of recognition of the Form and units employed by a PID algorithm can cause settings to be off by orders of magnitude.
Here we look at the Independent (Parallel) Form and how to convert settings to the ISA Standard Form that is also known as the Ideal Form. The answer also discusses the Series Form predominantly used in analog and early DCS controllers that is also known as the Interacting Form due to interaction of the derivative mode with the other modes settings in the time domain. Note that the tuning settings of the ISA Standard Form are non-interacting in the time domain but are interacting in the frequency domain. The inconsistent names for the Forms increase confusion.
ISA Mentor Program
The ISA Mentor Program enables young professionals to access the wisdom and expertise of seasoned ISA members, and offers veteran ISA professionals the chance to share their wisdom and make a difference in someone’s career. Click this link to learn more about the ISA Mentor Program.
Hector Torres’ Question
I am moving some PID currently residing in a PLC to a DCS. I would like taking advantage of the tuning already existing in the PLC to minimize commissioning time at startup. This is the information I got about this control loops in the PLC:
Loop 1:
PID Type: Independent
Control Action: E=PV-SP
Settings:
Proportional: 0.9
Integral: 0.75 repeats /min
Derivative: 0 min
Loop 2:
PID Type: Independent
Control Action: E=SP-PV
Settings:
Proportional: 1.5
Integral: 0.50 repeats/min
Derivative: 0 min
How can I translate these tuning parameters to a Form commonly used in a today’s DCS. I would like to use the Series Form of the PID. We are migrating from an older DCS that used the Series Form. The new DCS offers the ISA Standard Form and the Series Form.
Greg McMillan’s Answer
My understanding is that the independent PID is what is more commonly called the parallel PID because the contribution of the modes is independent in the time domain because the PID gain is not applied to the contribution from the integral and derivative modes (see Figure K-3 in Appendix K of Tuning and Control Loop Performance – Fourth Edition). Fortunately, your rate time is zero so we don't need to be concerned about whether you are using the Series or ISA Standard Form. The gain for the independent PID is the same as the ISA Standard PID and for the case of zero rate time is also the same as the Series Form. One thing to be careful about is to make sure the PLC algorithm is working with signals in percent rather than engineering units. Nearly all DCS and most PLC PID algorithms work with signals in percent. The user must thoroughly test and confirm all changes are correct by a real-time simulation before using them in an actual plant.
Assuming the proportional settings are a dimensionless gain and not Proportional Band, the PID algorithm works in percent signals and the Independent PID is what we call the Parallel Form, the equivalent Series Form settings are:
Loop 1:
Gain = 0.9
Reset = 0.9 * 60/0.75 = 0.9 * 80 = 72 sec
Rate = 0 sec
Loop 2:
Gain = 1.5
Reset = 1.5 * 60/0.5 = 1.5 * 120 = 180 sec
Rate = 0 sec
It would be good if Michel and/or Hunter would check these results in case I am missing something or am in error in some way.
Hunter Vegas’ Answer
I didn't work through Greg's numbers but generally when I am faced with something like this I have been able to find "conversions" from one system to another. You didn't specifically mention the PLC you were using but I have found tuning software packages can convert and even a scan on the internet can turn up some decent conversion equations. Do note that some PLCs have issues where scan time can alter the execution time of the PID block and effectively change your tuning constants accordingly.
Michel Ruel’s Answer
Be careful with terminology… most suppliers use independent for parallel and dependent for series but some suppliers use independent for ideal form and dependent for series. You need to look at the structure and read the description.
Greg McMillan’s Follow Up
If you scroll down on the webpage Comparison of PID Algorithms to the Parallel PID noted as the PID algorithm with “independence” you see the equations to convert from the Parallel Form to the Ideal Form (ISA Standard Form) are the same as the ones I used below and in my book but with different nomenclature. Some parallel algorithms have integral gain instead of an integral time (seconds) or the inverse of integral time (repeats/second) and a derivative gain rather than a derivative time. The general methodology is:
Use Chapter 1 Equation 1.2b to convert the integral mode reset setting from repeats per minute to seconds (seconds per repeat).
Use Appendix K Equations K.7, K.8, and K.9 to convert settings from the Parallel PID (Independent PID) to the ISA Standard Form (Ideal PID).
If the rate time is not zero and the integral time is much greater than four times the rate time, use Equations K.4, K.5, and K.6 to convert from the ISA Standard Form to the Series Form. Note that if the rate time is zero, Equations K.4 and K.5 show the Series Form settings are the same as the ISA Standard Form settings since the division by 2 is cancelled by the multiplication by 2.
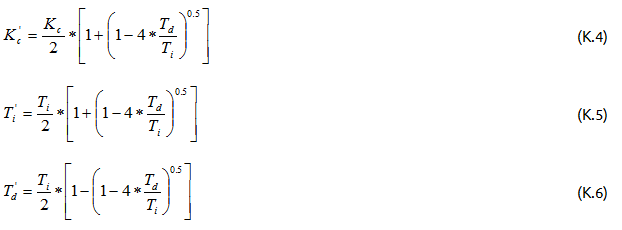
To convert the tuning settings from older DCS Series Form to the newer DCS default ISA Standard Form:
Note that if the rate time is zero, the ISA Standard Form and Series Form settings are identical because the correction factor applied becomes 1. When using the ISA Standard Form, if the rate time is greater than one-fourth the reset time the response can become oscillatory. If the rate time exceeds the reset time, the response can become unstable from a reversal of action from these modes. The Series Form inherently prevents this instability by increasing the effective reset time as the rate time is increased.
Nomenclature:
Additional Mentor Program Resources
See the ISA book 101 Tips for a Successful Automation Career that grew out of this Mentor Program to gain concise and practical advice. See the InTech magazine feature article Enabling new automation engineers for candid comments from some of the original program participants. See the Control Talk column How to effectively get engineering knowledge with the ISA Mentor Program protégée Keneisha Williams on the challenges faced by young engineers today, and the column How to succeed at career and project migration with protégé Bill Thomas on how to make the most out of yourself and your project. Providing discussion and answers besides Greg McMillan and co-founder of the program Hunter Vegas (project engineering manager at Wunderlich-Malec) are resources Mark Darby (principal consultant at CMiD Solutions), Brian Hrankowsky (consultant engineer at a major pharmaceutical company), Michel Ruel (executive director, engineering practice at BBA Inc.), Leah Ruder (director of global project engineering at the Midwest Engineering Center of Emerson Automation Solutions), Nick Sands (ISA Fellow and Manufacturing Technology Fellow at DuPont), Bart Propst (process control leader for the Ascend Performance Materials Chocolate Bayou plant), Angela Valdes (automation manager of the Toronto office for SNC-Lavalin), and Daniel Warren (senior instrumentation/electrical specialist at D.M.W. Instrumentation Consulting Services, Ltd.).
About the Author
Gregory K. McMillan, CAP, is a retired Senior Fellow from Solutia/Monsanto where he worked in engineering technology on process control improvement. Greg was also an affiliate professor for Washington University in Saint Louis. Greg is an ISA Fellow and received the ISA Kermit Fischer Environmental Award for pH control in 1991, the Control magazine Engineer of the Year award for the process industry in 1994, was inducted into the Control magazine Process Automation Hall of Fame in 2001, was honored by InTech magazine in 2003 as one of the most influential innovators in automation, and received the ISA Life Achievement Award in 2010. Greg is the author of numerous books on process control, including Advances in Reactor Measurement and Control and Essentials of Modern Measurements and Final Elements in the Process Industry. Greg has been the monthly "Control Talk" columnist for Control magazine since 2002. Presently, Greg is a part time modeling and control consultant in Technology for Process Simulation for Emerson Automation Solutions specializing in the use of the virtual plant for exploring new opportunities. He spends most of his time writing, teaching and leading the ISA Mentor Program he founded in 2011.
Image Source: Wikipedia








