This is from a series of articles reprinted from the journal ISA Transactions. All ISA Transactions articles are free to ISA members, or can be purchased from Elsevier Press.
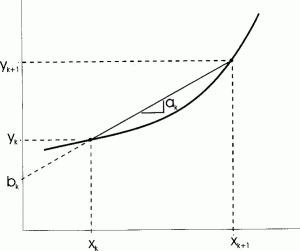
Abstract: Accurately determining the effect of the propagation of uncertainty in nonlinear applications can be awkward and difficult. The Monte Carlo approach requires statistically significant numbers of function evaluations (typically 105 or more) and analytical methods are intractable for all but the simplest cases. This paper derives and demonstrates a method to estimate the propagation of uncertainty in nonlinear cases by representing the function in a piecewise fashion with straight line segments. The probability density function of the result can be calculated from the transformation of the line segments. The mean and confidence intervals of the result can then be calculated from the probability density function. For the special case of a normal distribution in the independent variable, calculation of the mean and confidence intervals requires evaluation of only the error function (erf). A simple example is presented to demonstrate the technique. Variations on the basic approach are presented and discussed.
Free Bonus: To read the full article on estimating nonlinear uncertainty propagation, click here.
ISA membership entitles you to free access to all ISA Transactions articles plus a wealth of technical content, industry information, free webinars, training opportunities, program discounts, certification and licensure and professional networking.
Join ISA ... learn, advance, succeed!